The
Executable Object Command Language
Contents
- Introduction
- Working With Basic Elements
- Tables
- Sets
- Sequences
- A-Lists
- Iteration Expresions
- Variables and Scope
- Let Expressions
- Loops
- Operations
- Exception Handling
- Simple Dispatching
- Patterns
- Working With Syntax
- Quasi-Quotes and Lifting
- The XOCL Grammar
- Operation Grammar
Introduction
This book is about how to construct executable models. The previous sections have described with super-structure for creating these models. An action language is required to make models expressed in this super-stucture executable. The action language used in the rest of this book is called XOCL (eXectuable Object Command Language). It is one of the languages that can be embedded in the super-structure via the Performable class.There are many other languages that could be used with the super-structure, XOCL is general-purpose, other languages may be domain specific in the sense that their features would be familiar to a domain export or be tailored to a specific type of activity. Fortunately, XOCL is really all that is required since it has been designed to be extensible. XOCL is fully modelled within the super-structure: all of its features including syntax and execution semantics are defined using the super-structure and XOCL. Therefore, if XOCL is not the most suitable choice for a given application then it can be extended or even replaced.
This chapter defines the basic components of XOCL. It describes how XOCL fits into the super-structure and the key language constructs. The language features are given using examples. The following section describes how XOCL can be viewed as a model within the super-structure and how to extend it.
To top.
Working With Basic Elements
The simplest components of XOCL are constants (notice that comments follow // on a single line or within /* and */ over multiple lines as in Java):10 // An integer.
3.14159 // A float.
true // A boolean.
"Hello World" // A string.
context Root
@Operation prec(op)
@Case op of
"::" do 0 end
"." do 1 end
"+" do 3 end
"-" do 3 end
"*" do 4 end
"/" do 4 end
"=" do 5 end
"<>" do 5 end
"<" do 5 end
">" do 5 end
"<=" do 5 end
">=" do 5 end
"and" do 6 end
"andthen" do 6 end
"or" do 6 end
"orelse" do 6 end
"implies" do 7 end
":=" do 8 end
";" do 10 end
end
end
context Root
@Operation fact(n)
if n = 0
then 1
else n * fact(n - 1)
end
end
context Root
@Operation gcd(m:Integer,n:Integer):Integer
if m = n
then n
elseif m > n
then gcd(m-n,n)
else gcd(m,n-m)
end
end
context Root
@Operation addBits(n:Integer):Integer
if n = 0 or n < 0
then 0
else (n and 1) + (addBits(n.rsh(1)))
end
end
Integer division is performed by the operation div and floating point division is performed by the infix operator / (translating integers to floats as necessary). The operators sqrt, sin and cos are defined for floats.
All values in XMF support the operation 'of' that returns the most specific class of the receiver. A value can be asked whether it is of a given class using the operator isKindOf. Classes can be compared using inheritsFrom where a class is considered to inherit from itself. We could define isKindOf as:
context Element
@Operation isKindOf(type:Classifier):Boolean
self.of().inheritsFrom(type)
end
XMF strings are of type String. The following operation wraps the string "The" and "." around a supplied string:
context Root
@Operation makeSentence(noun:String):String
"The " + noun + "."
end
context Root
@Operation startsUpperCase(s:String):Boolean
if s->size > 0
then
let c = s->at(0)
in "A"->at(0) <= c and c <= "Z"->at(0)
end
else false
end
end
Since strings are compared on a character by character basis this makes string comparison relatively inefficient when performing many comparisons. Strings are often used as the keys in lookup tables (for example as the names of named elements). In order to speed up comparison, XMF provides a specialization of String called Symbol. A symbol is the same as a string except that two symbols with the same sequence of characters have the same identity. Comparison of symbols by identity rather than character by character is much more efficient. A string s can be converted into a symbol by Symbol(s).
Any value can be converted into a string using the operation toString. To get the string representation of a number for example: 100.toString()).
To top.
Tables
A table is used to associate keys with values. A table has operations to add associations between keys and values and lookup a given key. A table is created using the Table constructor supplying a single argument that indicates the approximate number of elements to be stored in the table. Suppose that a library maintains records on borrowers:context Root
@Class Library
@Attribute borrowers : Table = Table(100) end
end
context Library
@Operation newBorrower(id:String,name:String,address:String)
if not borrowers.hasKey(id)
then
let borrower = Borrower(id,name,address)
in borrowers.put(id,borrower)
end
else self.error("Borrower with id = " + id + " already exists.")
end
end
context Library
@Operation getBorrower(id:String):Borrower
if borrowers.hasKey(id)
then borrowers.get(id)
else self.error("No borrower with id = " + id)
end
end
context Library
@Operation idsInUse():Set(String)
borrowers.keys()
end
context Library
@Operation allBorrowers():Set(Borrower)
borrowers.values()
end
Sets
A set is an unordered collection of elements. The elements of a set need not all be of the same type. When T is the type of each element of the set then the set is of type Set(T). Operations are provided to add and remove elements from sets and to combine sets. Sets can be used in iterate expressions.Sets are created by evaluating a set expression of the form: Set{x,y,z,...} where x, y, z etc are element expressions. For example:
Set{1,true,Set{"a","b","c"},Borrower("1","Fred","3 The Cuttings")}
Suppose that the set operation {\tt includes} was not provided as part of XOCL. It could be defined by:
context Set(Element)
@Operation includes(e:Element):Boolean
if self->isEmpty
then false
else
let x = self->sel
in if x = e
then true
else self->excluding(x)->includes(e)
end
end
end
end
Sequences
A sequence is an ordered collection of elements. The elements in the sequence need not all be of the same type. When T is the type of each element in the sequence then the sequence is of type Seq(T). Sequences can be used in iterate expressions as described in section iterate.Sequences are created by evaluating a sequence expression or by translating an existing element into a sequence. Sets, strings, integers and vectors can be translated to sequences of elements, characters, bits and elements respectively by performing e.asSeq().
The following operations are defined on sequences: + appends sequences; asSet transforms a sequence into a set; asString transforms a sequence of character codes into a string; asVector transforms a sequence into a vector; at takes an index and returns the element at that position in the sequence, it could be defined as:
context Seq(Element)
@Operation at(n:Integer):Element
if self->size = 0
then self.error("Seq(Element).at: empty sequence.")
else if n <= 0
then self->head
else self->tail.at(n - 1)
end
end
end
context Seq(Element)
@Operation butLast():Seq(Element)
if self->size = 0
then self.error("Seq(Element)::butLast: empty sequence.")
elseif self->size = 1
then Seq{}
else Seq{self->head | self->tail->butLast}
end
end
context Seq(Element)
@Operation flatten():Seq(Element)
if self->isEmpty
then self
else self->head + self->tail->flatten
end
end
context SeqOfElement
@Operation indexOf(element:Element):Integer
if self = Seq{}
then -1
elseif self->head = element
then 0
else self->tail->indexOf(element) + 1
end
end
context Seq(Element)
@Operation hasSuffix(suffix):Boolean
self->reverse->hasPrefix(suffix->reverse)
end
context Seq(Element)
@Operation map(message:String . args:Seq(Element)):Element
self->collect(x | x.send(message,args))
end
context Seq(Element)
@Operation qsort(pred):Seq(Element)
if self->isEmpty
then self
else
let e = self->head
in let pre = self->select(x | pred(x,e));
post = self->select(x | x <> e and not pred(x,e))
in pre->sort(pred) + Seq{e} + post->sort(pred)
end
end
end
end
Seq{"Root","EMOF","Class","attributes"}->ref(Seq{Root})
The operation reverse reverses the receiver:
context Seq(Element)
@Operation reverse():Seq(Element)
if self->isEmpty
then Seq{}
else self->tail->reverse + Seq{self->head}
end
end
The operation subst takes three arguments: new, old and all; it returns the result of replacing element old with new in the receiver. If all is true then all elements are replaced otherwise just the first element is replaced.
The operation subSequence takes a staring and terminating indices and returns the appropriate subsequence; take takes an integer argument and returns the prefix of the receiver with that number of elements; tail returns the tail of a non-empty sequence.
Sequences have identity in XOCL; the head and tail of a sequence can be updated using:
S->head := e
S->tail := e
To top.
A-Lists
An a-list is a sequence of pairs; each pair has a head that is a key and a tail that is the value associated with the key in the a-list. A-lists are used as simple lookup tables. They are much more lightweight than instances of the class Table and have the advantage that the large number of builtin sequence operations apply to a-lists. The following class shows how an a-list can be used to store the age of a collection of people:context Root
@Class People
@Attribute table : Seq(Element) end
@Operation newPerson(name:String,age:Integer)
self.table := table->bind(name,age)
end
@Operation getAge(name:String):Integer
table->lookup(name)
end
@Operation hasPerson(name:String):Boolean
table->binds(name)
end
@Operation birthday(name:String)
// Assumes name is in table:
table->set(name,table->lookup(name) + 1)
end
end
Iteration Expressions
Iteration expressions in XOCL allow collections (sets and sequences) to be manipulated in a convenient way. Iteration expressions are a shorthand for higher-order operations that take an operation as an argument and apply the argument operation to each element of the collection in turn. As such, iteration expressions can be viewed as sugar for the invocation of the equivaent higher-order operations.A collection can be filtered using a select expression:
S->select(x | e)
context Seq(Element)
@Operation select(pred:Operation):Seq(Element)
if self->isEmpty
then self
elseif pred(self->head)
then Seq{self->head | self->tail.select(pred)}
else self->tail.select(pred)
end
end
context Set(Element)
@Operation reject(pred:Operation):Set(Element)
if self->isEmpty
then self
else
let x = self->sel
in if pred(x)
then self->excluding(x)->reject(pred)
else self->excluding(x)->reject(pred)->including(x)
end
end
end
end
S->collect(x | e)
context Seq(Element)
@Operation collect(map:Operation):Seq(Element)
if not self->isEmpty
then
let x = self->sel
in self->excluding(x)->select(map)->including(map(x))
end
else self
end
end
S->iterate(x y = v | e)
Seq{1,2,3,4,5}->iterate(i sum = 0 | sum + i)
context Seq(Element)
@Operation iterate(y:Element,map:Operation):Element
if self->isEmpty
then y
else self->tail.iterate(map(self->head,y),map)
end
end
C->collect(e | M) |
C->iterate(e c = o.of().default() | c->including(M)) |
C->exists(e | M) |
C->iterate(e b = false | b or M) |
C->forAll(e | M) |
C->iterate(e b = true | b and M) |
C->reject(e | M) |
C->iterate(e c = e.of().default() | if M then c else c->including(e) end) |
C->select(e | M) |
C->iterate(e c = e.of().default() | if M then c->includng(e) else c end) |
Variables and Scope
context Root
@Class Point
@Attribute x : Integer end
@Attribute y : Integer end
@Constructor(x,y) ! end
@Operation getX():Integer
x
end
@Operation getY():Integer
y
end
end
context Root
@Class Point
@Attribute x : Integer (?) end
@Attribute y : Integer (?) end
@Constructor(x,y) ! end
end
Dynamic variables are typically values associated with names in name-spaces. Dynamic variables are established when the association between the variable name and the value is created and typically persist for the rest of the lifetime of the XMF session. Lexical variables are typically created when values are supplied as arguments to an operation or when local definitions are executed. The association between the lexical variable name and the value persist for the duration of the operation definition or the execution of the body of the local block. In both cases, as the name suggests, variable values can change by side-effect.
A dynamic variable added to the Root name-space has global scope because Root is imported everywhere. A new dynamic variable in a name-space N is created as follows:
N::v := e;
import N in e end
To top.
Let Expressions
Lexical variables are established when arguments are passed to an operation or using a let expression. In both cases the variable can be referenced in the body of the expression, but not outside the body. In both cases the variables can be updated using v := e. Suppose we require an operation that takes two integers and returns a pair where the head is the smallest integer and the tail is the other integer:context Root
@Operation orderedPair(x,y)
let min = 0;
max = 0
in if x < y then min := x else min := y end;
if x > y then max := x else max := y end;
Seq{min | max}
end
end
context Root
@Operation orderedPair(x,y)
let min = if x < y then x else y end then
max = if min = x then y else x end
in Seq{min | max}
end
end
context Root
@Operation orderedPair(x,y)
let min:Integer = if x < y then x else y end then
max:Integer = if min = x then y else x end
in Seq{min | max}
end
end
context Root
@Operation max(s:Seq(Integer)):Integer
let max2(x:Integer,y:Integer):Integer =
if x > y
then x
else y
end
in s->iterate(n max = 0 | max2(max,n))
end
end
parserImport XOCL;
context Root
@Operation max(s:Seq(Integer)):Integer
@Letrec findMax(max:Integer,s:Seq(Integer)):Integer =
if s->isEmpty
then max
elseif s->head > max
then findMax(s->head,s->tail)
else findMax(max,s->tail)
end
in findMax(0,s)
end
end
Loops
XMF provides While and For for looping through collections and provides Find for selecting an element in a collection that satisfies a condition. A While loop performs an action until a condition is satisfied (not a named element may use a symbol for its name so we ensure the name is a string using the toString operation):context Root
@Operation findElement(N:Set(NamedElement),name:String)
let found = null
in @While not N->isEmpty do
let n = N->sel
in if n.name().toString() = name
then found := n
else N := N->excluding(n)
end
end
end;
found
end
end
context Root
@Operation findElement(N:Set(NamedElement),name:String)
let found = null
in @For n in N do
if n.name().toString() = name
then found := n
end
end;
found
end
end
let forColl = S;
isFirst = true
in @While not forColl->isEmpty do
let x = forColl->sel
in forColl := forColl->excluding(x);
let isLast = forColl->isEmpty
in e;
isFirst := false
end
end
end
end
context Seq(Operation)
@Operation toString()
let s = "Seq{"
in @For e in self do
s := s + e.toString();
if not isLast then s := s + "," end
end;
s + "}"
end
end
context Root
@Operation getNames(people:Seq(Person)):Seq(String)
@For person in people produce
person.name
end
end
context Root
@Operation createTable(names:Seq(String),addresses:Seq(String),telNos:Seq(String))
@For name,address,telNo in names,addresses,telNos produce
Seq{name,address,telNo}
end
end
context Root
@Operation addToAll(n:Integer,t:Table)
@For k in table.keys() do
k.put(k,t.get(k) + n)
end
end
context Root
@Operation addToAll(n:Integer,t:Table)
@For k inTableKeys table do
k.put(k,t.get(k) + n)
end
end
@Find(element,elements)
when element.name() = name
end
@Find(element,elements)
when element.name() = name
do "Candidate: " + element.name()
else throw NoCandidateFound()
end
@Count i from 0 to v->size do
v.put(i,v.get(i)+1)
end
Operations
XMF operations are used to implement both procedures and functions. An operation has an optional name, some parameters, a return type and a body. Operations are objects with internal state; part of the internal state is the name, parameter information, type and body. Operations also have property lists that can be used to attach information to the operation for use by XMF programs.Operations can be created and stored in XMF data items. In particular, operations can be added to name spaces and then referenced via the name space (either where the name space is imported or directly by giving the path to the operation). We have seen many examples of adding operations to the name space called Root. The syntax:
context Root
@Operation add(x,y) x + y end
Root.add(@Operation add(x,y) x + y end);
add.invoke(null,Seq{1,2})
add(1,2)
Lexically bound variables that are scoped over an operation are available within the body of the operation event though the operation is returned from the lexical context. This is often referred to as closing the lexical variable into the operation (or closure). This feature is very useful when generating behaviour that differs only in terms of context. Suppose that transition machine states have an action that is implemented as an operation and that the action is to be performed when the state is entered:
context StateMachines
@Class State
@Attribute name : String end
@Attribute action : Operation end
@Constructor(name,action) end
@Operation enter()
action()
end
end
myFormat(stdout,"Arg 1 = ~S, arg 2 = ~S~%",x,y)
context Root
@Operation myFormat(out:OutputChannel,control:String . args)
format(out,control,args)
end
context Root
@Operation o[callCount=0]()
o.setProperty("callCount",o.property("callCount") + 1);
// body of operation o...
end
context Root
@Operation mkPoint(x,y)
@Letrec newPoint =
@Operation[x=x,y=y](message . args)
@Case message of
"getX" do
newPoint.property("x")
end
"setX" do
newPoint.setProperty("x",args->head)
end
"getY" do
newPoint.property("y")
end
"setY" do
newPoint.setProperty("y",args->head)
end
end
end
in newPoint
end
end
To top.
Exception Handling
When an error occurs in XOCL, the source of the error throws an exception. The exception is a value that, in general, contains a description of the problem and any data that might help explain the reason why the problem occurred.An exception is thrown to the most recently established handler; intermediate code is discarded. If no handler exists then the XOCL VM will terminate. In most cases, the exception is caught by a user defined handler or, for example in the case of the XMF console, a handler established by the top level command interpreter.
When an exception is caught, the handler can inspect the contents of the exception and decide what to do. For example it may be necessary to re-throw the exception to the next-most recently established handler, since it cannot be dealt with. On the other hand, it is usual to catch the exception, print a message, patch up the problem, or just give up on the requested action.
For example, suppose that you have an application that reads data from a file. If the file does not exist then an exception is raised. This can be done as follows:
@Operation readData(file:String)
if file.fileExists()
then
// Read the data...
else self.error("The file does not exist.")
end
end
@Operation readData(file:String)
if file.fileExists()
then
// Read the data...
else throw Exception("The file does not exist.")
end
end
try
readData(someFile)
catch(x:Exception)
// Do something with x...
end
@Operation readData(file:String)
if file.fileExists()
then
// Read the data...
else throw FileNotFound(File)
end
end
try
readData(someFile)
catch(x:Exception)
@TypeCase(x)
FileNotFound do
// OK use a default data file...
readData(defaultFile)
end
else
// We cannot handle the exception so
// re-throw it to a less-specific handler...
throw x
end
end
| ArgTypeError |
Type checking is on and an
operation argument does not match the declared type. |
| ArityError |
Incorrect number of arguments
are supplied to an operation. |
| AttributeTypeException |
The type of an attribute cannot
be found when it is defined. |
| CaseFailed |
No case arm matched the value(s). |
| ClassInheritanceException |
One of the named parent classes
did not exist when a class was defined. |
| Error |
A general error. |
| Exception |
A general exception. |
| IndexOutOfBounds |
Illegal index for a collection. |
| LocalTypeError |
Type checking is on and a
let-bound variable value does not match the declared type. |
| MapFailed |
A mapping (like a
case-expression) contains no matching clause for the supplied values. |
| NameSpaceRef |
A name-space reference (e.g.
P::Q) could not be resolved. |
| NoKeyInTable |
A reference to a non-existent
key in a table. |
| NoOperation. |
A message is sent but no
matching operation is found. |
| NoSlot |
A slot reference is performed on
an object, but not slot is defined. |
| ResultTypeError |
Type checking is on and the
return value of an operation call does not match the declared type. |
| StringConversionError |
Converting a string to a type
was not possible. |
| TypeError |
An operation was attempted but
the element was not of the expected type. |
| UnboundVar |
The variable is not bound. |
To top.
Simple Dispatching
The type of an element is checked using the @TypeCase construct:@TypeCase(x)
String do
// Do something with a string...
end
Integer do
// Do something with an integer...
end
P::Q::X do
// Do something with an X...
end
else
// x was none of the above...
end
@Package Trees
@Class Tree
end
@Class Branch extends Tree
@Attribute left : Tree end
@Attribute right : Tree end
end
@Class Leaf extends Tree
@Attribute data : Element end
end
end
import Trees;
context Root
@Operation flatten(t:Tree)
@CaseObj(tree)
Branch[left,right] do
flatten(left) + flatten(right)
end
Leaf[data] do
Seq{data}
end
end
end
- The types referenced in a caseobj-expression (Branch and Leaf above) must be the direct types of the object; and
- The slots can only be bound by name (they cannot be sub-patterns).
@CaseInt[256] c of
0 do
// handle the 0-case...
end
1 to 100 do
// Handle the range 1 to 100...
end
101 to 200, 234 do
// Handle the range 101 to 100 and the
// value 234 ...
end
else
// None of the above matched...
end
To top.
Patterns
A pattern is matched against a value. The pattern match may succeed or fail in a given matching context. A matching context keeps track of any variable bindings generated by the match and maintains choice points for backtracking if the current match fails.Pattern matching can be viewed as being performed by a pattern matching engine that maintains the current pattern matching context as its state. The engine state consists of a stack of patterns to be matched against a stack of values, a collection of variable bindings and a stack of choice points. A choice point is a machine state. At any given time there is a pattern at the head of the pattern stack and a value at the head of the value stack. The machine executes by performing state transitions driven by the head of the pattern stack: if the outer structure of the pattern matches that of the value at the head of the value stack then:
- 0 or more values are bound.
- 0 or more choice points are added to the choice point stack.
- 0 or more component patterns are pushed onto the pattern stack.
- 0 or more component values are pushed onto the value stack.
A variable pattern consists of a name, optionally another pattern and optionally a type. The simplest form of variable pattern is just a name, for example, the formal parameter x is a variable pattern:
let add1 = @Operation(x) x + 1 end in ...
let add1 = @Operation(x:Integer) x + 1 end in ...
A constant pattern is either a string, an integer, a boolean or an expression (in the case of an expression the pattern consists of [ followed by an expression followed by ]). A constant pattern matches a value when the values is equal to the constant (in the case of an expression the matching process evaluates the expression each time the match occurs). For example:
let fourArgs = @Operation(1,true,"three",x = [2 + 2]) x end in ...
fourArgs(1,true,"three",4)
let head = @Operation(Seq{head | tail}) head end in ...
let add3 = @Operation(Seq{x,y,z}) x + y + z end in ...
A constructor pattern matches an object. A constructor pattern may be either a by-order-of-arguments constructor pattern (or BOA-constructor pattern) or a keyword constructor pattern. A BOA-constructor pattern is linked with the constructors of a class. It has the form:
let flatten = @Operation(C(x,y,z)) Seq{x,y,z} end in ...
A keyword constructor pattern has the form:
let flatten =
@Operation(C[name=y,age=x,address=y])
Seq{x,y,z}
end
in ...
A conditional pattern consists of a pattern and a predicate expression. It matches a value when the value matches the sub-pattern and when the expression evaluates to true in the resulting variable context. For example:
let repeat = @Operation(Seq{x,y} when x = y) Seq{x} end in ...
Set patterns consist of an element pattern and a residual pattern. A set matches a pattern when an element can be chosen that matches the element pattern and where the rest of the set matches the residual pattern. For example:
let choose = @Operation(S->including(x)) x end in ...
let chooseBigger =
@Operation(S->including(x),y where x > y)
x
end
in ...
chooseBigger(Set{1,2,3},2)
The following is an example that sorts a set of integers into descending order:
context Root
@Operation sort(S)
@Case S of
Set{} do
Seq{}
end
S->including(x) when S->forAll(y | y <= x) do
Seq{x | Q} where Q = sort(S)
end
end
end
context Root
@Operation remove0s(x)
@Case x of
(S1 when S1->forAll(x | x <> 0)) +
(S2 when S2->forAll(x | x = 0)) +
(S3 when S3->forAll(x | x <> 0)) do
S1 + S3
end
end
end
- Operation Parameters. Each parameter in an operation definition
is a pattern. Parameter patterns are useful when defining an operation
that must deconstruct one or more values passed as arguments. Note that
if the pattern match fails then the operation invocation will raise an
error. Operations defined in the same class and with the same name are
merged into a single operation in which each operation is tried in turn
when the operation is called via an instance of the class. Therefore in
the following example:
an instance of P has a single operation f that adds up all the elements of a sequence.@Class P
@Operation f(Seq{}) 0 end
@Operation f(Seq{x | t}) x + self.f(t) end
end - Case Arms. A case expression consists of a number of arms each of
which has a sequence of patterns and an expression. A case expression
dispatches on a sequence of values and attempts to match them against
the corresponding patterns in each arm in turn. For example, suppose we
want to calculate the set of duplicated elements in a pair of sets:
context Root
@Operation dups(s1,s2)
@Case s1,s2 of
s1->including(x),s2->including(y) when x = y do
Set{x} + dups(s1,s2)
end
s1->including(x),s2 do
dups(s1,s2)
end
s1,s2->including(y) do
dups(s1,s2)
end
Set{},Set{} do
Set{}
end
end
end
Working With Syntax
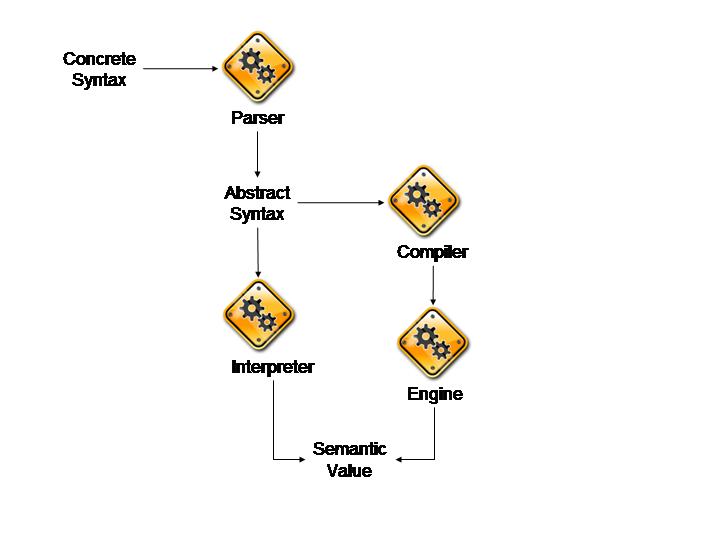
An element is performable if it can be requested to do two tasks: compile itself to a sequence of machine instructions and evaluate itself to produce an element. In many ways these two tasks are similar since compilation is translation from an element in one language to an element in another; the instructions in the machine language can each be asked to evaluate themselves. In order to design and develop language constructs it is important to understand how to process syntax; this section describes how XMF represents syntax and the various ways of transforming and evaluating syntax.
Figure is an overview of the key syntax processes. Processing starts with concrete syntax which is represented as a sequence of characters. The characters may originate from a variety of sources including files, strings or typed at a keyboard. A parser is a processing engine that transforms a sequence of characters into data elements; the data elements are referred to as abstract syntax.
Once syntax is represented in data, it can be processed in many different ways. It can be transformed from one representation to another. It can be analysed to see if it contains any errors. It can be executed directly. The figure shows two different ways of evaluating syntax: interpretation and compilation.
An interpreter is a program that takes another program as input and runs it. An interpreter typically requires extra input to describe the context of evaluation (for example the values for gobal variables in the program). An interpreter is a program that itself must be written in a language. The XOCL interpreter is written in XOCL and is easy to extend.
A compiler is a program that translates a supplied program from a source language to a target language. Typically the target language has an interpreter which is somehow better than any interpreter for the source language. For example the source language may not have an interpreter or the target interpreter is much faster than any source interpreter. In this case the XOCL compiler translates XOCL source into XMF VM instructions for which there is an interpreter written in Java. The XOCL compiler is written in XOCL and is easy to extend.
Every element that is to be used as syntax must implement the Performable interface. Performable, requires that a syntax element knows how to evaluate itself and how to compile itself. The interface is defined as follows:
Performable::compile(env,frame,isLast,saveSource)
// Produces a sequence of machine instructions.
// The env binds variable names that are currently
// in scope to type descriptors. The frame is an
// integer describing how many enclosing operations
// there are. isLast is true when there is nothing
// further to perform. saveSurce is true when operations
// are to make theor source code available at run-time.
Performable::eval(target,env,imports)
// Evauates the element to produce a value. The target
// is the value of 'self' during evaluation. The
// environment associates variable names with values.
// The imports are a sequence of imported name spaces.
Performable::FV()
// Returns a set of the free variables in the
// receiver.
Performable::maxLocals()
// Returns the maximum number of loal variables that
// is required in order to evaluate the receiver.
Performable::pprint(out,indent)
// Writes a textual version of the syntax to the
// output channel using indent as the current level
// of indentation after newlines.
The instructions produced by compiling a while-loop involve skip-instructions. The class While is a sub-class of Performable with performable attributes for the while-test and the while-body:
context While
@Operation compile(env,frame,isLast,saveSource)
let testCode = test.compile(env,frame,false,saveSource);
bodyCode = body.compile(env,frame,false,saveSource);
testLabel = Compiler::newLabel();
endLabel = Compiler::newLabel() then
returnValue = Compiler::labelInstrs(Seq{PushTrue()},endLabel)
in Compiler::labelInstrs(testCode,testLabel) +
Seq{SkipFalse(endLabel)} +
bodyCode +
Seq{Pop()} +
Seq{SkipBack(testLabel)} +
returnValue
end
end
Not all occurrences of a while-loop need to be compiled before they can be performed. Expressions typed at the top-level of XMF are not compiled, they are parsed to produce syntax objects and then evaluated. It is also possible to evaluate the source code in a file directlry without having to compile it. The definition of eval for a while-loop is given below:
context While
@Operation eval(target,env,imports)
@While test.eval(target,env,imports) do
body.eval(target,env,imports)
end
end
A free variable is one that is used by a perfomable element, but which is not locally defined by that element. In order to support compilation, each performable elment must define FV. Since a while-loop does not make direct reference to variables, the free variables are the union of those for the test and body:
context While
@Operation FV():Set(String)
test.FV() + body.FV()
end
context While
@Operation maxLocals():Integer
test.maxLocals().max(body.maxLocals())
end
context While
@Operation pprint(out,indent)
format(out,"@While ");
test.pprint(out,indent);
format(out," do~%~V",Seq{indent + 2});
body.pprint(out,indent + 2);
format(out,"~%~Vend",Seq{indent})
end
context Let
@Operation compile(env,frame,isLast,saveSource)
let valueCode = bindings->reverse->collect(b |
b.value.compile(env,frame,false,saveSource))->flatten;
letEnv = env.allocateLocals(bindings.name),env.maxLocal())
in valueCode +
// Generate SETLOC instructions...
letEnv.setLocalsCode(bindings.name) +
body.compile(letEnv,frame,isLast,saveSource)
end
end
context Let
@Operation eval(target,env,imports)
let newEnv = bindings->iterate(b e = env |
e.bind(b.name,b.value.eval(target,env,imports)))
in body.eval(target,newEnv,imports)
end
end
context Let
@Operation FV():Set(String)
bindings->iterate(binding FV = body.FV() - bindings.name->asSet |
FV + binding.value.FV())
end
context Let
@Operation maxLocals():Element
let valueMaxLocals = bindings->collect(b |
b.value.maxLocals())->max;
bindingMaxLocals = bindings->size;
bodyMaxLocals = body.maxLocals()
in valueMaxLocals.max(bindingMaxLocals + bodyMaxLocals)
end
end
context Let
@Operation pprint(out,indent)
format(out,"let ");
if bindings.isKindOf(Seq(Element))
then
@For b in bindings do
b.pprint(out,indent + 4);
if not isLast
then format(out,";~%~V",Seq{indent + 4})
else format(out,"~%~V",Seq{indent})
end
end
else bindings.pprint(out)
end;
format(out,"in ");
body.pprint(out,indent + 3);
format(out,"~%~Vend",Seq{indent})
end
The class defining the Object Command Language are defined in section .
Fortunately, it is not usually necessary to define the complete Performable interface for each new syntax class. This is because a new syntax class can be defined in terms of a translation to existing syntax classes that already implement the interface. This process is called desugaring and is covered in section . Desugaring involves trnslating from one abstract syntax to another. A useful technology to do this is quasi-quotes and this is the subject of the next section.
- Sugar
- Syntax
- Syntax Constants
- Exp
Quasi-Quotes and Lifting
Suppose that we have a requirement for a new syntax for an until-loop. An until-loop has the usual semantics and the syntax class has a body and a test, both of which are performable. The syntax class Until can fully implement the Performable interface, however, there is sufficient syntax constructs in XOCL to support until-loops in terms of while-loops. A traslation can be defined as follows:context Until
@Operation translateToWhile(body,test)
Order(body,While(test,body))
end
1. The concrete syntax of object construction.
2. The abstract syntax of a command followed by a while-loop.
When examples get a little larger than the one above, these issues become very confusing. XMF provides technology to address this issue: quasi-quotes. Quasi-quotes provide a means to construct syntax templates. The body of transateToWhile can be viewed as a syntax template: the fixed parts of the template are the ordering and the while-loop; the variable parts are the supplied body and test. Quasi-quotes allow the variable parts to be dropped into the fixed parts which are expressed using concrete syntax. Here is the same operation using quasi-quotes:
context Until
@Operation translateToWhile(body,test)
[| <body>;
@While <test> do
<body>
end
|]
end
A typical pattern that occurs when working with syntax involves a sequence of performable elements. Consider translating a sequence of elements to produce a single expression that performs each expression in order:
@Operation orderCommands(commands:Seq(Performable))
commands->iterate(command ordered = [| null |] |
[| <ordered>; <command> |])
end
@GuardedOp name(arg:type)
body
end
@Operation guardedOp(name:String,
arg:String,
type:Performable,
body:Performable)
[| @Operation <name>(<arg>)
if <Var(arg)>.isKindOf(<type>)
then <body>
else <Var(arg)>.error("Not of type " + <type>.toString())
end
end
|]
end
@Operation translateWith(object:Performable,
class:Class,
body:Performable)
class.allAttributes()->iterate(a exp = body |
let name = a.name().toString()
in [| <name> = <object>.<name> in <exp> end |]
end
)
end
@Operation translateWith(object:Performable,
class:Class,
body:Performable)
let A = class.allAttributes() then
updateSlots = A->iterate(a exp = [| withResult |] |
let name = a.name().toString()
in [| withObject.<name> := <Var(name)>; <exp> |]
end
) then
completeBody = [| let withResult = <body>
in <updateSlots>
end |]
in [| let withObject = <object>
in <A->iterate(a exp = completeBody |
let name = a.name().toString()
in [| let <name> = withObject.<name>
in <exp>
end |]
end
)>
end
|]
end
end
translateWith(
[| node.position |],
Point,
[| x := x + 1; y := y + 1; Seq{x,y} |])
let withObject = node.position
in let x = node.position.x
in let y = node.position.y
in let withResult = x := x + 1;
y := y + 1;
Seq{x,y}
in withObject.x := x;
withObject.y := y;
withResult
end
end
end
end
The XOCL Grammar
@Grammar
AddPattern ::=
// An add pattern may use the infix + operator to specify
// that the pattern matches a collection split into two...
p1 = AtomicPattern
( '+' p2 = AddPattern { Addp(p1,p2) }
| { p1 }
).
AName ::=
// Often it is desirable to allow a name to be
// specified as a dropped string, as in <s>....
Name! | Drop.
Apply ::=
// An application may be a simple atomic expression
// followed by some arguments and then optionally
// followed by an arrow ->...
a = Atom e = ApplyTail^(a) Arrow^(e).
ApplyTail(a) ::=
args = Args! { Apply(a,args) }
| args = KeyArgs! { Instantiate(a,args) }
| { a }.
Arrow(a) ::=
'->' ! ArrowTail^(a)
| { a }.
Args ::= '(' ArgsTail.
ArgsTail ::=
')' { Seq{} }
| arg = Expr args = (',' Expr)* ')' { Seq{arg | args} }.
ArrowTail(c) ::=
n = Name x = CollOp^(c,n) Arrow^(x).
Atom ::=
// An atomic expression is self contained an involves no
// infix operators. Notice the use of ! to force the parse
// to be deterministic in case any of the different types
// of atomic expression start with the same terminals...
VarExp!
| Self!
| StrExp!
| IntExp!
| IfExp!
| BoolExp!
| LetExp!
| CollExp!
| Parentheses
| Drop
| Lift
| Throw
| Try
| ImportIn
| FloatExp
| LocalParserImport
| AtExp.
AtExp ::=
// An at-expression causes the parser to dispatch to
// another grammar for the scope of the @ ... end. The
// Terminal '@' is used in XOCL to introduce an at-expression,
// however this is not necessary - you could use any
// terminal to introduce an at-expression...
l = LinePos '@' e = @ { e.setLine(l) }.
AtomicPattern ::=
// An atomic pattern is one that is delimited and is
// not followed by a pattern infix operator...
Varp
| Constp
| Objectp
| Consp
| Keywordp
| Syntaxp
| '(' Pattern ')'.
Binding ::=
// A binding is a name followed by a value expression...
name = AName BindingTail^(name).
BindingTail(name) ::=
// A binding may be a value binding or may introduce
// an operation...
BindFun^(name)
| BindValue^(name).
BindFun(name) ::=
args = BindFunArgs type = OptType '=' value = SimpleExp { FunBinding(name,args,type,value) }.
BindFunArgs ::=
'(' BindFunArgsTail.
BindFunArgsTail ::=
p = Pattern ps = (',' Pattern)* ')' { Seq{p | ps} }
| ')' { Seq{} }.
BindValue(name) ::=
// A value binding is a name, optionally a type designator and
// the value...
type = OptType '=' value = SimpleExp { ValueBinding(name,type,value) }.
BindingList ::=
// Bindings in parallel are separated by ';' (note that sequential
// bindings are sneakily processed in the parser by flattening
// let-expressions)...
binding = Binding bindings = (';' Binding)* { Seq{ binding | bindings } }.
Bindings ::=
// You can drop a complete binding list into a
// let-expression...
BindingList
| Drop.
BinOp ::=
// Binary operators are parsed with equal precedence. The
// operator associativity rules and precedence rules are
// organised by an abstract syntax tree transformation that
// occurs post parsing (called from the parser) using a
// syntax walker...
'<' { "<" }
| '<=' { "<=" }
| '>' { ">" }
| '>=' { ">=" }
| '<>' { "<>" }
| '=' { "=" }
| '::' { "::" }
| ':=' { ":=" }
| '.' { "." }
| 'and' { "and" }
| 'andthen' { "andthen" }
| 'implies' { "implies" }
| 'or' { "or" }
| 'orelse' { "orelse" }
| '+' { "+" }
| '-' { "-" }
| '*' { "*" }
| '/' { "/" }.
BoolExp ::=
l = LinePos 'true' { BoolExp(l,true) }
| l = LinePos 'false' { BoolExp(l,false) }.
Boolp ::=
'true' { Constp(BoolExp(true)) }
| 'false' { Constp(BoolExp(false)) }.
CollExp ::=
SetExp!
| SeqExp!.
CollOp(c,n) ::=
// Handling the different types of syntax construct
// that can occur after a ->...
CollMessage^(c,n)
| Collect^(c,n)
| Iterate^(c,n)
| { CollExp(c,n,Seq{}) }.
CollMessage(c,n) ::=
'(' as = CommaSepExps ')' { CollExp(c,n,as) }.
Collect(c,n) ::=
'(' v = AName '|' e = Expr ')' { IterExp(c,n,v,e) }.
CommaSepExps ::=
e = Expr es = (',' Expr)* { Seq{e | es} }
| { Seq{} }.
CompilationUnit ::=
// A compilation unit is essentially a file full of
// definitions with parser imports and name-space
// imports at the head of the file...
// Parser imports affect the current parse...
ParserImport*
// Name-space imports affect the dynamic variables
// referenced in the rest of the compilation unit...
imports = Import*
// A sequence of definitions ot expressions...
exps = CompilationBody*
// The end of the input...
EOF
s = pState
{ CompilationUnit("",imports,exps,s.getSource()) }.
CompilationBody ::=
// An element in a compilation unit...
Def
| TopLevelExp.
Consp ::=
// A sequence pattern...
Pairp
| Seqp
| Emptyp.
Constp ::=
// A constant pattern...
Intp
| Strp
| Boolp
| Expp.
Def ::=
// A definition is introduced into a compilation
// unit using the keyword 'context'. Essentially this
// just adds a value to the container designated by
// the path. The initialization of the value is suppressed
// using the optional ! modifier...
'context'
// If ! is supplied then the expression
// may contain forward references and therefore
// the value is not initialized. The value should
// be initialized by other means (for example
// explicitly) at some later point...
isForward = ('!' { true } | { false })
// The path designates a container...
path = ImportPath
// The value of the expression is added to
// the container...
exp = Exp { ContextDef(path,exp,isForward) }.
Drop ::=
// A dropped value lives in < and > and a
// dropped pattern lives in <| and |>. Note
// that the call of resolve and order are
// used to transform an expression with respect
// to operator associativity and precedence...
'<' e = DropExp '>' { Drop(resolve(order(e))) }
| '<|' p = Pattern '|>' { DropPattern(p) }.
DropExp ::=
// We need to be careful inside dropped expressions
// because > is used as a terminator and not an
// operator...
'not' e = DropExp { Negate(e) }
| a = Apply DropExpTail^(a).
DropExpTail(a) ::=
o = DropOp! e = DropExp { BinExp(a,o,e) }
| { a }.
DropOp ::=
// Omit the > since this is a terminator
// for a dropped expresssion...
'<' { "<" }
| '<=' { "<=" }
| '<>' { "<>" }
| '=' { "=" }
| '::' { "::" }
| ':=' { ":=" }
| '.' { "." }
| 'and' { "and" }
| 'andthen' { "andthen" }
| 'implies' { "implies" }
| 'or' { "or" }
| 'orelse' { "orelse" }
| '+' { "+" }
| '-' { "-" }
| '*' { "*" }
| '/' { "/" }.
EImport ::=
'import' exp = TopLevelExp { Evaluator::Import(exp) }.
Emptyp ::=
// Essentially a constant pattern...
'Seq{' '}' { Constp(SetExp("Seq",Seq{})) }
| 'Set{' '}' { Constp(SetExp("Set",Seq{})) }.
EmptySeqTail(l) ::=
'}' { SetExp(l,"Seq",Seq{}) }.
EvaluationUnit ::=
// An evaluation unit is similar to a compilation
// unit but is used to construct a component that
// can evaluated (instead of compiled)...
ParserImport*
imports = EImport*
exps = (Def | TopLevelExp)*
EOF
{ Evaluator::EvaluationUnit(imports,exps) }.
Exp ::=
// The usual entry point when parsing a single
// expression. Note that the resolve and order
// operators are used to transform the abstract
// syntax tree in order to implement the rules
// of operator associativity and precedence. Note
// also that resolve and order *must* be called
// somewhere, therefore if you use a different
// clause as your entry point then you may need
// to call these explicitly yourself...
e = Expr! { resolve(order(e)) }.
Expr ::=
// Expr is used throughout the grammar as the clause
// that produces a general expression. The difference
// between Exp and Expr is that the order and resolve
// operations are *not* called by Expr since these
// need only be called once for the root expression...
'not' e = Expr { Negate(e) }
| '-' e = SimpleExp { BinExp(IntExp(0),"-",e) }
| a = Apply ExpTail^(a).
ExpTail(a) ::=
o = Op! e = Expr { BinExp(a,o,e) }
| { a }.
Exp1 ::=
// Use Exp1 if you require all of the input to be
// consumed by the parser...
Exp EOF.
Expp ::=
// A pattern that evaluates a component expression
// and then compares the result with the supplied
// value...
'[' exp = Exp ']'
{ Constp(exp) }.
FloatExp ::=
l = LinePos f = Float
{ f.lift().line := l }.
IfExp ::=
// An if-expression starts with 'if' and
// 'then'. After these have been consumed
// there are a number of alternative forms...
l = LinePos
'if' e1 = Expr
'then' e2 = Expr
e3 = IfTail
{ If(l,e1,e2,e3) }.
IfTail ::=
// An if-expression may have an optional 'else'
// and may nest using 'elseif'...
'else' Expr 'end'
| l = LinePos 'elseif' e1 = Expr 'then' e2 = Expr e3 = IfTail { If(l,e1,e2,e3) }
| 'end' { BoolExp(false) }.
Import ::=
'import' path = ImportPath ';' { Import(path) }.
ImportPath ::=
n = Name ns = ('::' Name)* { Seq{n | ns} }.
ImportIn ::=
'import' path = ImportPath 'in' body = Exp 'end' { ImportIn(path,body) }.
IntExp ::=
l = LinePos e = Int { IntExp(l,e) }.
Intp ::=
i = Int { Constp(IntExp(i)) }.
Iterate(c,n) ::=
'(' v1 = AName v2 = AName '=' init = Expr '|' body = Expr ')'
{ Iterate(c,v1,v2,init,body) }.
KeyArgs ::=
// Keyword arguments occur in keyword instantiation
// expressions...
'[' (']' { Seq{} }
| arg = KeyArg args = (',' KeyArg)* ']' { Seq{arg | args} }).
KeyArg ::=
name = Name '=' exp = Expr
{ KeyArg(name,exp) }.
Keywordp ::=
// A keyword instantiation pattern that matches an
// object that is an instance of the classifier
// designated by the path and whose slots match
// the patterns designated by the keyword patterns...
name = Name names = ('::' Name)* '[' keys = Keyps ']'
{ Keywordp(name,names,keys) }.
Keyps ::=
key = Keyp keys = (',' Keyp)* { Seq{key | keys} }
| { Seq{} }.
Keyp ::=
name = Name '=' pattern = Pattern
{ Keyp(name,pattern) }.
LetBody ::=
// A let-expression may contain sequential bindings using
// the 'then' keyword. These are flattened in the parser
// by nesting let-expressions...
'in' body = Expr { body }
| 'then' bindings = Bindings body = LetBody { Let(bindings,body) }.
LetExp ::=
// A let-expression parses includes some bindings and then
// a body. The body may include some sequential bindings that
// are desugared in the parser as nested let-expressions...
l = LinePos
'let' bindings = Bindings
body = LetBody 'end'
{ Let(l,bindings,body) }.
Lift ::=
l = LinePos
'[|' e = Exp '|]'
{ Lift(l,e) }.
LocalParserImport ::=
// A local parser import allows name-spaces to be added
// to the current parse for use when at-expressions are
// encountered...
'parserImport'
name = Name names = ('::' Name)*
{ Seq{name | names} }
ImportAt
'in' e = Expr 'end'
{ ParserImport(Seq{name | names},e) }.
LogicalExp ::=
// Sometimes used as an entry point to avoid the use
// of ';'...
e = SimpleExp
{ resolve(order(e)) }.
NonEmptySeqTail(l) ::=
e = Expr
PairOrElements^(l,e).
Objectp ::=
// An object pattern involves a path that designates a
// class and a sequence of patterns. The class should define
// a constructor with the same arity as the number of
// patterns. The constructor is used to designate the slots
// whose values are matched against the component patterns...
name = Name names = ('::' Name)*
'(' slots = Patterns ')'
{ Objectp(name,names,slots) }.
Op ::=
BinOp!
| ';' { ";" }.
OpType ::=
// Operations can be specified to have a type that defines
// their argument types and their return type...
domains = TypeArgs '->' range = TypeExp { OpType(domains,range) }.
OptType ::=
// A binding may onclude an optional type after ':'...
':' TypeExp
// The syntax construct NamedType defaults the path
// to XCore::Element...
| { NamedType() }.
PairOrElements(l,e) ::=
'|' t = Expr '}'
{ ConsExp(e,t) }
| es = (',' Expr)* '}'
{ SetExp(l,"Seq",Seq{e|es}) }.
Pairp ::=
'Seq{' head = Pattern '|' tail = Pattern '}'
{ Consp(head,tail) }.
ParserImport ::=
// A parser import occurs at the head of a compileration or evaluation
// unit and adds a name-space to the current collection of name-spaces
// used to resolve the paths found in at-expressions...
'parserImport'
name = Name names = ('::' Name)* ';'
// construct the path...
{ Seq{name | names} }
// Add the name-space designated by the path to the
// current parse engine...
ImportAt.
Parentheses ::=
// Retain the user's parentheses since they are important
// when processing the syntax tree with respect to associativity
// and precedence rules...
'(' e = Expr ')'
{ Parentheses(e) }.
PathExp ::=
// A path expression is rooted in an atom (usually a variable)
// and followed by a sequence of names...
atom = Atom
( '::' name = AName names = ('::' AName)*
{ Path(atom,Seq{name | names}) }
| { atom }).
Pattern ::=
p = AddPattern
es = PatternTail*
p = { es->iterate(e s = p | Includingp(s,e)) }
PatternGuard^(p).
PatternGuard(p) ::=
'when'
e = Exp
{ Condp(p,e) }
| {p}.
PatternTail ::=
'->' Name '(' p = Pattern ')'
{ p }.
Patterns ::=
head = Pattern tail = (',' Pattern)* { Seq{head | tail} }
| { Seq{} }.
Self ::=
l = LinePos
'self'
{ Self(l) }.
SetExp ::=
// Note that set-expressions are used to represent
// both sets and (proper) sequences. The difference
// in the abstract syntax is designated by "Set" or
// "Seq"...
l = LinePos
'Set{' es = CommaSepExps '}'
{ SetExp(l,"Set",es) }.
SeqExp ::=
// A seq-expression starts with a Seq( and then
// may be empty, a pair, or a proper sequence...
l = LinePos
'Seq{'
(EmptySeqTail^(l) | NonEmptySeqTail^(l)).
Seqp ::=
'Seq{'
head = Pattern
tail = SeqpTail
{ Consp(head,tail) }.
SeqpTail ::=
',' head = Pattern
tail = SeqpTail
{ Consp(head,tail) }
| '}'
{ Constp(SetExp("Seq",Seq{})) }.
SimpleExp ::=
'not' e = SimpleExp { Negate(e) }
| '-' e = SimpleExp { BinExp(IntExp(0),"-",e) }
| a = Apply SimpleExpTail^(a).
SimpleExpTail(a) ::=
o = BinOp! e = SimpleExp { BinExp(a,o,e) }
| { a }.
StrExp ::=
l = LinePos
e = Str
{ StrExp(l,e) }.
Strp ::=
s = Str
{ Constp(StrExp(s)) }.
Syntaxp ::=
'[|' e = Exp '|]'
{ Syntaxp(e) }.
Throw ::=
l = LinePos
'throw'
value = SimpleExp
{ Throw(l,value) }.
TopLevelExp ::=
s = SimpleExp ';'
{ resolve(order(s)) }.
TopLevelCommand ::=
c = SimpleExp
p = pState
{ p.consumeToken := false } ';'
{ resolve(order(c)) }.
TypeExp ::=
// Type-expressions designate classifiers. They are either
// named (via paths), parametric (a classifier applied to
// some arguments) or an operation type...
path = TypePath (args = TypeArgs { ParametricType(path,args) }
| { NamedType(path) })
| Drop
| OpType.
TypeArgs ::=
'(' arg = TypeExp
args = (',' TypeExp)* ')'
{ Seq{arg | args} }.
TypePath ::=
name = Name names = ('::' Name)*
{ Seq{name | names}->collect(n | Symbol(n)) }.
Try ::=
l = LinePos
'try'
body = Expr
'catch'
'(' name = Name ')'
handler = Expr
'end'
{ Try(l,body,name,handler) }.
VarExp ::=
name = Name
l = LinePos
{ Var(name,l) }.
Varp ::=
name = AName
pattern =
( '=' Pattern
| { null }
)
type =
( ':' TypeExp
| { NamedType() }
)
{ Varp(name,pattern,type) }.
end
Operation Grammar
@Grammar extends OCL::OCL.grammar
Operation ::=
// The name of an operation is optional. If
// specified it can be a dropped string...
name = OpName
// Properties are optional in [ and ]...
ps = Properties
// Args must be specified, but may have optional
// types and the optional multiple argument at the
// end after a '.' ...
'(' args = OpArgs multi = OpMulti ')'
// The return type of an operation is optional...
type = ReturnType
// The body of an operation is a sequence of
// expressions...
body = Exp+
'end'
// Get the current parse state so that we can get
// hold of the current imports...
p = pState
// Create the operation...
{ ps->iterate(p x = Operation(name,args + multi,type).add(body).setIsMultiArgs(not multi->isEmpty).setImports(p.imports->excluding(XCore)->excluding(Root)->map("pathSeq")) |
[| <x>.setProperty(<StrExp(p->at(0))>,<p->at(1)>) |]
)
}.
OpName ::=
// An operation name is optional. It may be a
// dropped string or just a name. If a name is
// not specified then the name anonymous is used...
name = AName { if name.isKindOf(String) then Symbol(name) else name end }
| { Symbol("anonymous") }.
OpArgs ::=
arg = OpArg args = (',' OpArg)* { Seq{arg | args } }
| { Seq{} }.
OpArg ::=
// Operation arguments are patterns. If you
// want to drop a pattern in then it requires a ! in front...
Pattern
| '!' Drop.
OpMulti ::=
// Multi-arg operations have the final argument after
// a '.'. At run-time the rest of the supplied arguments
// are supplied as a sequence...
'.' multi = Pattern { Seq{multi} }
| { Seq{} }.
ReturnType ::=
':' TypeExp
| { NamedType() }.
Properties ::=
'[' p = Property ps = (',' Property)* ']' { Seq{p|ps} }
| { Seq{} }.
Property ::= n = Name '=' e = Exp { Seq{n,e} }.
end