Languages
Contents
- Introduction
- Everything is an Elementt
- Indexing Things
- Naming Things and Looking Them up
- Classifying Things
- Collections of Things
- Classifying Objects
- Performing Things
Introduction
In order for a language to be at all useful it must mean something. Meaning is a difficult thing to grasp since in order to talk about it at all it is necessary to use language which itself involves a question of meaning. However, it is possible to set down some broad ground-rules that can be used to establish a basic framework.First of all, a language has a syntax which comes in two flavours: concrete and abstract. Concrete syntax is how you read or write a language, it tends to be human-centric. The following is an example of concrete syntax:
x + 1
Abstract syntax deals with how a language is represented as data; it tends to be computer-centric. Here is the equivalent example represented as abstract syntax (think of the Java data structure that is created rather than the characters making up the program):
new BinExp(new Var("x"),PLUS,new Int(1))
The process by which concrete is turned into abstract syntax is called parsing. This book deals with models of languages and provides a great deal of examples of grammars that specify how to turn concrete into abstract syntax language representations.
Next, the syntax of a language does not define its meaning any more than you can judge a book by its cover. In order to have meaning, a language must have a semantic domain. A semantic domain is a model of the elements that the language denotes. A semantic domain for natural language (such as English) contains all the real-world concepts you can think of (such as Elephants and houses) in addition to all the conceptual things you can think of; in fact, it contains anything you can think of.
Languages used for system development are much more controlled in terms of syntax and semantics than natural languages. The semantic domains of such languages are defined by data types for elements appropriate to the systems domain. The particular data types depend on the system domain, for example a language for expressing telecoms will have a semantic domain containing networks, routers and devices. Languages defined for general use have general purpose semantic domains containing such things as records, integers, strings, events etc.
Finally, the meaning of a language is not defined by its syntax or its semantics alone; the meaning is the mapping that links the syntax to the semantics. In terms of modelling languages the mapping is often static, for example linking class definitions to sets of objects that are the instances of the classes. This of UML-style class models. What is the meaning of such a model? Since the class diagram does not specify any behaviour, neither does the semantics. a suitable semantics might be all the objects that can be constructed whose structure matches that specified in the class model. For programming languages the mapping is dynamic since it links programs to execution traces and all the execution machinery that lives in the traces.
To understand a language you must be fluent in its syntax, its semantic domain and the mapping between them.
This book is about techniques for modelling aspects of systems. This book is not about how you analyse the systems themselves in order to model them; there are plenty of books about that topic. This book aims to provide a collection of techniques that allow you to raise the abstraction-bar when addressing system development issues.
When modelling systems it is desirable to focus on what is being expressed rather than how the information is being represented. This is the essence of a language driven approach to modelling: we can use high-level abstractions to capture the information without worrying about unnecessary implementation detail. The language that will be used to represent the information in this book is designed to provide a wide range of high-level constructs for modelling information.
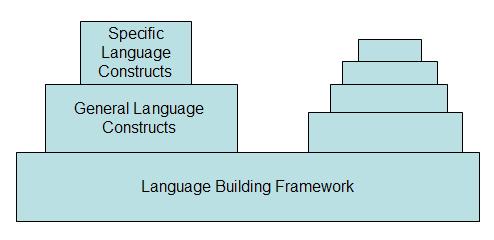
Furthermore, the language has been specifically designed to be extensible: if no language construct is provided to express the required information then the user can extend the language with a new construct that does the job. This is the ball-of-mud model first pioneered by the Lisp family of programming languages. Rather than being a pejorative term, a language is like a ball of mud when new features can be added to the language in a way that the new features become part of the language and are indistinguishable from the existing features. No special actions need to be taken to use the new extensions: they have been seamlessly integrated into the language.
Rather than being a ball of mud, it is possible to view the different languages as towers as shown in figure . The base level is a very general language that supports the construction of other language (ideally it will support the definition of itself). A language is grown from the basic framework by adding successive layers of language constructs; each layer is built from all those layers below it and the layers become progressively more tailored to specific application domains. The ball of mud principle is maintained when the addition of a layer does not preclude the use of constructs from lower layers and when languages build in different towers can be used in the same application.
This chapter defines the semantic domain for the language that is used throughout the rest of the book. The next chapter describes the syntax of the language XOCL. The chapter after than describes language building features. On reading the rest of this chapter you should expect to appreciate the key data values that can be expressed and the kind of operations that are applied to the values. Each major category of value has a section to itself.
The element types are divided into groups described in the following sections. In each case the types that form a coherent aspect of the semantic domain are grouped together. An overview of the aspect is given along with a collection of operations that make up an interface for the group. Note that the interface is very general; it is intended that a given application will extend this interface by dynamically adding more operations to the domain types as required.
To top.
Everything is an Element
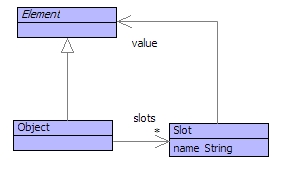
Figure shows the root class of the value domain: everything is an element - some things are objects. When designing the value domain we had a choice: should everything be an object? Objects have state represented as slots; a slot has a name and a value. The slots of an object can be updated. Objects have an identity: when you create an object it will be different to every other object that you have ever created (even if the slots are the same).
But not all values have changeable state and an identity. For example: the integer 3. Does it make sense to talk of the state of 3? Does it make sense to change the state of 3? Given two occurrences of 3, are they the same or not?
The distinction between Element and Object allows us to make the distinction between values whose state cannot change and which have no identity. Therefore, 3 is an element, but not an object. A set is an element and not an object, as is a string and a boolean value.
Our language is object-oriented and computation proceeds by message passing. When an element is sent a message, if its type defines an operation with the same name as the message then the operation defines the actions that are performed. If T defines an operation o expecting argments (x,y,z) then T::o(x,y,z) is the operation. In the rest of this chapter each section defines some types; the key operations for the types are described; where the type of arguments or the return type of an operation is Element then the type is omitted.
The main operations defined by Element are:
Element::copy():Element
// Returns a copy of the receiver.
Element::equals(other):Boolean
// Returns true when the arg is equal
// to the receiver.
Element::init()
// Initializes the receiver.
Element::isKindOf(type:Classifier):Boolean
// Returns true when the receiver is an
// instance of the supplied type.
Element::of():Classifier
// Returns the type of the receiver.
Element::toString():String
// Returns a string representation
// of the receiver.
Object::get(name:String)
// Return the value of the slot or throw
// an error if the slot does not exist.
Object::hasSlot(name:String):Boolean
// Returns true when the receiver has a
// slot with the given name.
Object::set(name:String,value)
// Updates the given slot or throws an
// error if the slot does not exist.
Indexing Things
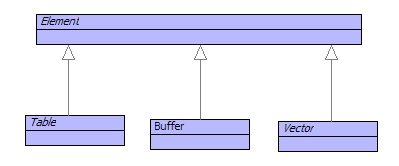
When dealing with values it is desirable to build collections where the elements in the collection are indexed by a key. The key is specified when the element is placed into the collection and the key is used to look the element up in the collection. The value associated with a key in a collection may be changed.
Figure shows three classes that are used to represent basic indexed collections. Notice these classes extend Element, not Object, therefore these indexed collections have no slots. A table uses any element as a key, buffers and vectors use integers as keys. The difference between a buffer and a vector is that the former grows to accommodate elements as they are added whereas the latter is a fixed size.
What would you use these for? A table is useful when building arbitrary associations, for example associating names of personnel with their employment records. Vectors are useful when you know the size of the collection in advance, for example the locations on a chess board. Buffers are useful when you need the collection to grow as required and want to index elements by their position, for example building an output string.
The main table operations are as follows:
Table(n:Integer):Table
// Returns a table. The argument indicates the
// likely max keys.
Table::clear()
// Empties the receiver.
Table::get(key)
// Returns the value of the key or raises
// an error if the key is not present.
Table::hasKey(key):Boolean
// Returns true when the key is in the table.
Table::keys():Set(Element)
// Returns the keys in the table.
Table::put(key,value)
// Updates the table.
Table::remove(key)
// Removes the key from the table.
Table::values():Set(Element)
// Returns the set of values in the table.
Buffer(n:Integer,isString:Boolean):Buffer
// Returns a buffer. The first arg is the size to
// grow by each time the buffer is extended. The
// second indicates whether the buffer is a string
// buffer or a general buffer.
Buffer::add(element)
// Adds the element to the end of the buffer.
Buffer::append(s:String)
// Appends the chars to the end of a string buffer.
Buffer::asSeq():Seq(Element)
// returns the buffer as a sequence.
Buffer::at(i:Integer)
// Returns the element at index i or throws an error
// if the buffer has no element at position i.
Buffer::size():Integer
// Returns the number of elements currently in
// the buffer.
Vector(n:Integer):Vector
// Returns a new vector of the specified size.
Vector::asSeq():Seq(Element)
// Returns the vector as a sequence.
Vector::put(element,index:Integer)
// Updates the vector at the specified index or
// throws an error if the index is out of range.
Vector::ref(i:Integer)
// Returns the element at the specified index.
Vector::size():Integer
// Returns the size of the vector.
Naming Things and Looking Them Up
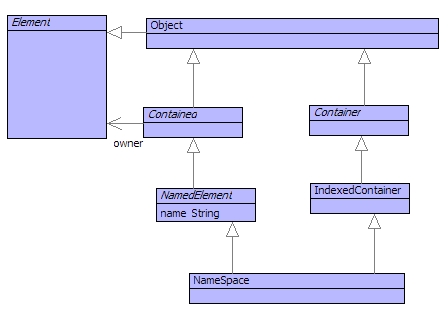
Elements are often identified by their name and the value domain provides special support for named elements and their containers. Figure shows the classes that define these elements. A contained element has a link to its owner and a named element is a contained element with a name. A container is a class that wraps up internal storage implemented by tables, vectors and the like. An indexed container is a wrapper for a table (allowing users to extend the class). A name space is a named element that contains other named elements.
Notice that the structure of a name space allows name spaces to contain other name spaces. This means that references to named elements may cross a number of nested name spaces, leading to the idea of a path to an element. There is always a global name space called Root in the value domain: everything is contained in Root. A path is a sequence of names separated by '::'. So Root::X references the named element with the name X in the name space Root. If X is a name space containing a named element Y then the path is Root::X::Y. Since Root is special, it can be omitted: X::Y.
The main operations defined by Contained are:
Contained::owner()
// Returns the owner of the receiver.
Contained::setOwner(owner)
// Updates the owner.
Container::add(element)
// Adds the element to the receiver.
Container::allContents():Set(Element)
// Returns all the elements directly
// or indirectly contained by the receiver.
Container::contents():Set(Element)
// Returns the direct contents of the
// receiver.
Container::includes(element):Boolean
// Returns true when the receiver
// contains the element.
Container::remove(element)
// Removes the element from the
// receiver.
NamedElement::name():String
// Returns the name.
NamedElement::path():String
// Returns the path through name-spaces to
// the receiver.
NamedElement::pathSeq():Seq(String)
// Returns the path through name-spaces to
// the receiver as a sequence of strings.
NamedElement::setName(name:String)
// Updates the name of the receiver.
IndexedContainer():IndexedContainer
// Creates and returns an indexed container.
IndexedContainer::add(key,value)
// Updates the indexed container.
IndexedContainer::index(key)
// Returns the indexed value or throws
// an error.
Classifying Things
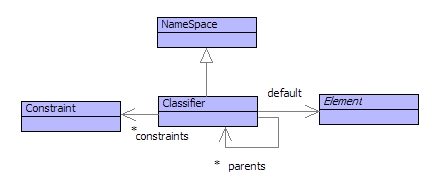
The values in a value domain fall into different groups: the integers, the objects, the personnel records, the update events etc. Each of these groups is a type and there is an element that represents the type: a classifier. A classifier is a single value that defines characterising features of a group of values: its instances. Each instance in the group refers to the classifier as its type. For example the integer 3 has Integer as its type. Furthermore, sub-groups can often be identified such that elements of a sub-group have more characterising features - this is specialization.
Figure shows the classes that define classification. A classifier defines a collection of constraints: rules that govern the characterising features of its instances. A classifier has parents, the child parents are spcializations of the parent classifiers. All the constraint rules of the parents are used to classify the instances of the child classifier which may add rules of its own. Finally, a classifier has a default element, for example the classifier Integer has a default value of 0.
Classifier defined the following operations:
Classifier::new()
// Return a new instance of the receiver.
Classifier::new(args:Seq(Element))
// Return a new instance of the receiver
// after it is initialized using the args.
Classifier::invoke(target,args:Seq(Element))
// Same as using new.
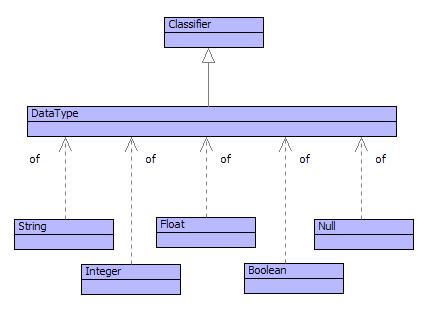
The basic data values such as 10, true and ``a string'' are all classified by distinguished classifiers Integer, Boolean and string. These classifiers, in turn are classified by the classifier DataType as shown in figure . The special value null is classified by Null; it is used as the default value for all values that have internal state.
The types String, Integer, Float, Boolean and Null each define their own collection of operations that are listed in the appendix.
To top.
Collections of Things
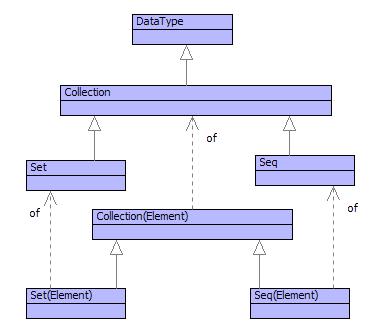
Two types of non-indexed collections are very useful: sets and sequences. A set is an unordered collection, adding the same element to a set has no effect and it is not possible to rely on the order of elements in a set. The following is a set of integers: Set{1,2,3,4}, it is the same set as Set{4,3,2,1} and the set Set{1,1,3,2,3,4}. Figure shows the classifiers that apply to sets and sequences. In general the classifier of a set of elements of type T is Set(T); since everyting is classified by Element then the most general set-based classifier is Set(Element).
A (non fixed size) sequence is either empty Seq{} or is a value v followed by a sequence s: Seq{v | s}. A sequence has a head, v, and a tail, s. Sequences lend themselves to recursive processing by case analysis on the empty sequence and the non-empty sequence. Sequences of elements of type T are classified by type Seq(T) and the most general sequence classifier is Seq(Element).
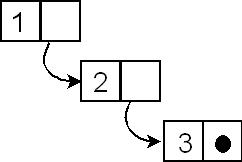
Figure shows the sequence Seq{1,2,3} which is equivalent to the sequence Seq{1 | Seq{2 | Seq{3 | Seq{}}}}. The head of the sequence is the integer 1 and the tail of the sequence is Seq{2,3}. The final dot in the figure represents the empty sequence Seq{}.
Sequences of element are used heavily in this book to represent collections. They are built-in to the implementation of the language and cannot be extended. The appendix lists many of the operations that are provided for manipulating sequences.
To top.
Classifying
Objects
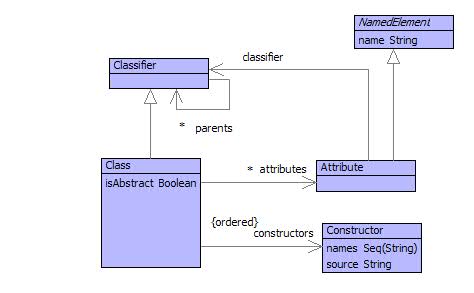
Objects are values with identity and state. The identity is set when the object is created and the state is represented as a collection of slots. Each slot has a name and a value. Objects are used to represent elements with properties, for example personnel records have personnel properties including the name of the employee, salary and department. Objects can be used to represent real-world things such as companies or products and can be used to represent abstract things such as colours (with red, green and blue properties) and system models.
Figure shows the classes that are used to classify objects. The classifier of an object is a class with attributes that classify the slots of the object. Each attribute has a name (defining the name of the slot that the attribute classifies) and a type that classifies the value of the slot. A class may be abstract in which case it does not directly classify any objects, but may have sub-classes (linked via the parents attribute from Classifier) whose direct instances it classifies.
Each class has a number of constructors. Each constructor is a rule that defines how a new instance of the class is created. A constructor has a sequence of names that must correspond to the names of the attributes defined (or inherited) by the class. When a constructor is used to create an instance of a class it is supplied with values for each of its names. A new instance of the class is created and the slots with the corresponding names are initialized from the supplied values. Each new instance will have a new identity. Constructors are inherited from the parents of a class and there is always a constructor (inherited from Object) that has no names.
To top.
Performing
Things
The domain described so far contains elements that represent data, but
nothing that actually does anything. It is possible to inspect the
value of an object's slot and update it, but there is no domain element
that represents what happens when an object receives a message. the
value domain contains operations that, upon being supplied with
argument values, perform actions. The actions that can be performed are
describes in the next section; this section describes the basic
structure of an operation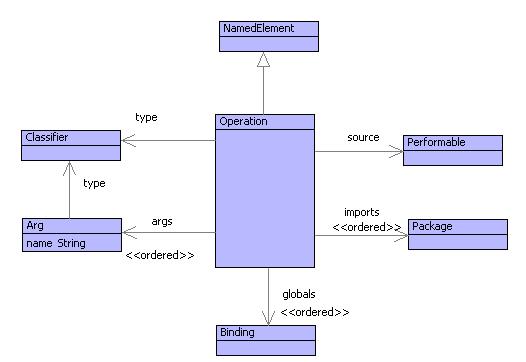
Figure shows the classes that define the tructure of an operation. Each operation is a named element that can be placed into a name space. An operation has a return type and a sequence of typed arguments. The source of an operation is a performable element; this is the source code of the operation that is performed then the operation is invoked.
Within the source there may be variable references. A variable reference may correspond to an argument, a name from an imported name space (called a dynamic variable), or a variable that was in scope when the operation was created (called a global variable). Each of these categories of variable are described with respect to examples in the next section.
Operations give us the ability to run programs. furthermore, there is no restriction on where an operation can live in the value domain: operations may be placed as the values of slots, may be added to collections or may be placed in tables. Furthermore, all data values have to come into existence somehow: they are produced by performing the actions in an operation. Even operations come into existence this way.
To top.