Graphs

Overview

Unfortunately, information is not always conveniently organised in a tree structure. A tree structure does not make allowances for relationships that span the tree or where cycles occur in the data. For example, what happens when a company employee fills two roles within the company in different departments? It would be approprate for the employee to occur underneath both departments in the tree; the employee is shared between the departments or equivalently there are two different paths from the root of the tree to the employee.

Trees do not represent sharing and multiple paths very well. There are strategies; for example, XML is a tree structured data format where labels are used to mark up the elements in order to represent sharing. When data representation requires sharing, it is usually because the data naturally forms a graph. Graphs can be encoded in trees (and other forms of data representation), but if the data requires a graph then it is probably best to use one and be done with it.

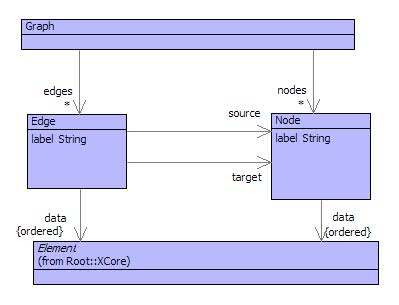
Graphs

Figure  shows a model of graphs. A graph consists of a set of nodes and a set of edges. Each node has a label and a sequence of data. The label is used to identify the node and the data is used by applications for whatever purpose they require.

Each edge has a label and data, and also has a source and target node. Edges go between nodes and are directed. The diagram shown in figure  is itself an example of a graph where the nodes are displayed as class boxes and the edges are shown as attribute edges. Notice that the node labelled Element is shared (parent-wise) between Edge and Node; equivalently there are two paths from the rot node (labelled Graph) to the node labelled Element: Graph, Edge, Element and Graph, Node, Element. Such sharing is difficult to represent using trees.

Graphs are a very rich form of data representation. There is a wealth of material written about graphs and how to process them. Here are some useful operations on graphs defined in XOCL:
context Graph
  @Operation nodeFor(label:String):Node
    @Find(node,nodes)
      when node.label() = label
      else null
    end
  end
The operation nodeFor returns the node with the supplied label, or null if no such node exists. The operation edgesFrom returns the set of edges from a given node:
context Graph
  @Operation edgesFrom(n:Node):Set(Edge)
    edges->select(e | e.source() = n)
  end
Graphs are generally useful and therefore it is appropriate to have a general purpose language construct to define a graph. As mentioned above, each use of a graph structure will attach different amounts of data to the nodes and labels. The data is used to support the application specific processing of the graph. Therefore, a general purpose language construct for graph construction should support:
  1. Arbitrary node and edge data.
  2. Plug-points for the sub-classes of Graph, Node and Edge that are used to represent the graph.
Here are two examples of different graph applications:
@Graph(Routes,Location,Road)
  London()
    M1(200) -> Leeds
    A1(50)  -> Cambridge
end

@Graph(Plan,Task,Dependency)
  Start("January")
    -> Contractors
    -> Plans
  Contractors("March")
  Plans("April")
end
The first graph is represented as an instance of the class Routes where the nodes and edges are instances of the classes Location and Road. These classes are sub-classes of Graph, Node and Edge repsectively. Locations have no data; the three locations have labels London, Leeds and Cambridge.

An edge is listed below the source node. In the first example graph, there are two edges with labels M1 and A1. The edges have data 100 and 50 (being the distance in miles) and the label of the edge target is givn after ->.

The second example is a plan graph. The nodes have data that represents the month at which the task is completed. Edges have no labels or data (they just represent dependencies).

The proposed structure for a graph definition has plug-points for the graph, node and edge classes and a body consisting of a sequence of node definitions. A node definition n is a node label, followed by node data in parentheses followed by a series of edge definitions for which the source of the node is n. An edge definition is an optional edge label, optional edge data in parentheses, an arrow and then the label of the target node. Here is an example:
@Graph(G,N,E)
  n1(a,b,c)
    e1(d) -> n2
    e2() -> n3
  n2()
    e3() -> n1
  n3()
end
When the parser encounters a graph definition it will synthesize program code that, when evaluated, produces the required graph. Are there any rules that need to be observed when this synthesis takes place? Given the model of graphs in figure , a graph contains nodes and edges, and edges link nodes. Here is a possible program that produces the graph above:
(1) let g = G()
(2) in g.addToNodes(N("n1",Seq{a,b,c}));
       g.addToNodes(N("n2"));
(3)    g.addToNodes(N("n3"));
(4)    g.addToEdges(E("e1",Seq{d},g.nodeFor("n1"),g.nodeFor("n2")));
       g.addToEdges(E("e2",g.nodeFor("n1"),g.nodeFor("n3")));
(5)    g.addToEdges(E("e3",g.nodeFor("n2"),g.nodeFor("n1")));
(6)    g
    end
Line (1) creates the graph using the supplied class G (a sub-class of Graph). Each node must be added first in lines (2-3) so that edges can then be created between the nodes in lines (4-5). Note that the supplied classes N and E are used to create the nodes and edges. Finally the graph is returned in line (6).

The rules for graph construction are: create the graph, add the nodes and then add the edges. Unfortunately, the graph definition construct does not follow this pattern; it interleaves node and edge definitions. A strategy is required to untangle this interleaving.

One way to address the interleaving is to have the parser synthesize an intermediate graph definition that is processes using two or more passes. This is perfectly respectable, and often a sensible way forward when the required processing is fairly complex.

In this case, the processing is not that complex, so another strategy is used. To see how this works, a few definitions are required. An edge constructor expects a graph and an edge class; it adds some edges to the supplied graph. A node constructor expects a graph, a node class, an edge class and a collection of edge constructors; it adds some nodes to the supplied graph and then uses the edge constructor to add some edges.

Node definitions are synthesized into node constructors and edge definitions into edge constructors. The trick is to build up the edge constuctors so that they are performed after all the node constructors. Since the edge constructors are supplied to the node constructors, this should be easy. Using the running example from above:
n3 =
  @Operation(nodeConstructor)
    @Operation(g,N,E,edgeConstructor)
      g.addToNodes(N("n3"));
      nodeConstructor(g,N,E,edgeConstructor)
    end
  end
The node definition for n3 is transformed into an operation that is supplied with a node constructor and returns a node constructor. This construction allows n3 to be linked with other noe constuctors without knowing any details -- i.e. n3 can be defined in isolation.

The node constructor for n2 is similar, but involves the addition of an edge constructor:
n2 =
  @Operation(nodeConstructor)
    @Operation(g,N,E,edgeConstructor)
      let e3 = 
        @Operation(g,E)
          g.addToEdges(E("e3",g.nodeFor("n2"),g.nodeFor("n1")))
        end
      in g.addToNodes(N("n2"));
         nodeConstructor(g,N,E,addEdges(edgeConstructor,e3))
      end
    end
  end
Note how the edge constructor for e3 is added to the supplied edge contructor (using the yet-to-be-defined addEdges) when the supplid node constructor is activated. This is the key to deferring the construction of edges until all the nodes have been defined.

What should addEdges do? It is used to link all the edge constructors together so that they all get activated. It takes two edge constructors and returns an edge constructor:
@Operation addEdges(ec1,ec2)
  @Operation(g,E)
    ec1(g,E);
    ec2(g,E)
  end
end
The node constructor for n1 is similar, but two edge constructors are required:
n1 =
  @Operation(nodeConstructor)
    @Operation(g,N,E,edgeConstructor)
      let e1 = 
        @Operation(g,E)
          g.addToEdges(E("e1",g.nodeFor("n1")Seq{d},g.nodeFor("n2")))
        end;
          e2 = 
        @Operation(g,E)
          g.addToEdges(E("e1",g.nodeFor("n1"),g.nodeFor("n3")))
        end then
          edges = addEdges(e1,e2)
      in g.addToNodes(N("n2"));
         nodeConstructor(g,N,E,addEdges(edgeConstructor,edges))
      end
    end
  end
The complete graph can now be defined by linking the node constructors together and supplying a graph:
let nc = addNodes(n1,addNodes(n2,addNodes(n3,noNodes)))
in nc(G(),N,E,@Operation(g,E) g end)
end
Each of the node constructors are linked via an operation addNodes. The left-hand argument of addNodes is an operation that maps a node constructor to a node constructor. The right-hand argument is a node constructor. It is easier to see how this works from the definition:
@Operation addNodes(nodeCnstrCnstr,nodeCnstr2)
  @Operation(g,N,E,edgeConstructor)
    let nodeCnstr1 = nodeCnstrCnstr(nodeCnstr2)
    in nodeCnstr1(g,N,E,edgeConstructor)
    end
  end
end
The mechanism used by addNodes is an example of a typical pattern that threads sequences of operations together. It allows the node constuctor encoded in nodeCnstrCnstr to occur before that encoded in nodeCnstr2 while also allowing the edge constructors produced by the first to be handed on to the second (because they are to be deferrred until all the nodes are added to the graph).

There are two types of constructor, each of which can occur repeatedly in a sequence: nodes and edges. When this occurs, it is usual to have some way to encode an empty sequence; in this case there are noNodes and noEdges. Both of these are constructors:
@Operation noNodes(g,N,E,edgeConstuctor)
  edgeConstructor(g,E)
end

@Operation noEdges(g,E)
  null
end
noNodes is a node constructor that starts edge construction. Therefore, noNodes should be the right-most node constuctor in a sequence that is combined using addNodes. noEdges does nothing, and can occur anywhere in a sequence.

The grammar for graph definition synthesizes node and edge constructors combined usin addNodes and addEdge. When an empty sequence is encountered, the gramar synthesizes noNodes and noEdges respectively. The grammar is defined below:
@Grammar extends OCL::OCL.grammar

    Data ::= 
 
      // The data associated with a node or edge
      // is a sequence of elements... 
 
      '(' es = CommaSepExps ')' 
 
      { SetExp("Seq",es) }.

    Edges(s) ::= 
 
      e = Edge^(s) 
 
      es = Edges^(s)
 
      { [| addEdges(<e>,<es>) |] } 

    | { [| noEdges |] }.

    Edge(s) ::= 
 
      l = Label 
 
      d = OptData 
 
      '->' t = Label 
 
      { [| 
           @Operation(g,E)
             g.addToEdges(E(<l>,<d>,g.nodeFor(<s>),g.nodeFor(<t>)))
           end 
        |] 
      }.

    Graph ::= 
 
       // A graph consists of three constructor
       // operations...
 
      '(' mkGraph = Exp 
 
         ',' mkNode = Exp 
 
         ',' mkEdge = Exp
 
      ')' 
 
      // ... followed by the node and edge
      // definitions...

      GraphBody^(mkGraph,mkNode,mkEdge).

    GraphBody(mkGraph,mkNode,mkEdge) ::=
 
      // The graph body consists of the node and
      // edge definitions. An expression is synthesized
      // that constructs the graph using continuation
      // passing...
 
      ns = Nodes 'end' 
 
      { [| 
           <ns>(<mkGraph>(),<mkNode>,<mkEdge>,@Operation(g,E) g end) 
        |] 
      }.

    Label ::= 
 
      NameExp 
 
    | { "".lift() }.

    NameExp ::= 
 
      n = Name 
 
      { n.lift() }.

    Nodes ::= 
 
      n = Node 
 
      ns = Nodes
 
      { [| addNodes(<n>,<ns>) |] } 

    | { [| noNodes |] }.

    Node ::= 
 
      l = Label 
 
      d = Data 
 
      e = Edges^(l) 
 
      { [|
           @Operation(Cn)
             @Operation(g,N,E,Ce)
 
               // Create the node using the constructor
               // and then add the edges...

               g.addToNodes(N(<l>,<d>));
               Cn(g,N,E,addEdges(<e>,Ce))
             end
           end
        |] 
      }.

    OptData ::= 
 
      Data 
 
    | { [| Seq{} |] }.

  end